Not all the electrons in the core remnant are degenerate to begin with. As has been noted, the surface of the white dwarf is still very hot, giving the surface electrons enough energy to be in higher energy states. However, these electrons radiate energy, and with no thermonuclear reactions to replenish it, fall into lower energy states. Once an electron is in the lowest energy state possible it can no longer radiate energy. The white dwarf’s luminosity hence decreases with time, until it becomes cold and dark.
There is a maximum limiting mass for the existence of a white dwarf, and this was calculated mathematically by Subrahmanyan Chandrasekhar. To follow the calculation, first consider the equations for hydrostatic equilibrium.
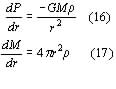
and to close the system of equations, let

Combining (16) and (17), we get
![]()
Defining a dimensionless radius and density:
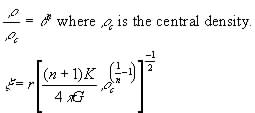
Equation (18) and the boundary conditions become
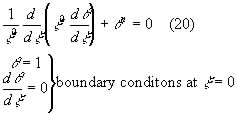
This is called the polytropic equation of index n, and by looking at the first zero of ![]() the relationships between pressure, density, radius and mass. The densities of the gas and its pressure can be calculated by using the number density for the Fermi momentum, giving pressure by equations (10) and (11). This gives electron pressures of the form:
the relationships between pressure, density, radius and mass. The densities of the gas and its pressure can be calculated by using the number density for the Fermi momentum, giving pressure by equations (10) and (11). This gives electron pressures of the form:
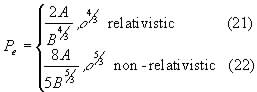
where A, and B are constants containing the masses and the ionisation of the particles concerned. It can be seen that these are polytropes. By substituting equation (21) into the polytrope and numerically solving it, a maximum mass of 1.4 solar masses is found.