In the case of an isotropic material both surface tension and diffusivity are independent of the crystalline orientation and are given by ![]() and
and ![]() , say. This evolution equation becomes
, say. This evolution equation becomes
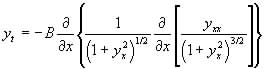 (6)
(6)
where ![]() . No analytic solutions are known for equation (6) (Cahn & Taylor, 1994). Mullins (1957) assumed the surface slope was everywhere small,
. No analytic solutions are known for equation (6) (Cahn & Taylor, 1994). Mullins (1957) assumed the surface slope was everywhere small, ![]() which gives the linearised equation
which gives the linearised equation
![]() . (7)
. (7)
Tritscher (1996a) showed that (7) was also an integrable form of the governing equation (5) for a class of anisotropic materials with behaviour similar to a liquid crystal and constitutive relations
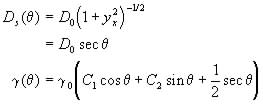 (8)
(8)
where C1 and C2 are arbitrary constants and ![]() is the solution of the Herring equation (Herring, 1951)
is the solution of the Herring equation (Herring, 1951)
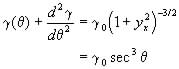 (9)
(9)
By use of symmetry recursion operators applied to the linearizable nonlinear diffusion equation Broadbridge & Tritscher (1996) derived a further linearizable form of the evolution equation
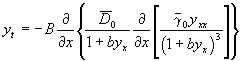 (10)
(10)
where ![]() are weights for the surface diffusivity and surface tension and b is an arbitrary parameter which orients the crystalline lattice relative to the coordinate axis. The constitutive relations for equation (10) are (Tritscher, 1996)
are weights for the surface diffusivity and surface tension and b is an arbitrary parameter which orients the crystalline lattice relative to the coordinate axis. The constitutive relations for equation (10) are (Tritscher, 1996)
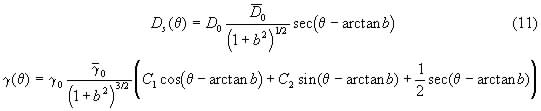
The constitutive functions show degeneracy and for values of b less than around ![]() the evolution equation satisfactorily models an isotropic material.
the evolution equation satisfactorily models an isotropic material.