The evolution equation (10) of Tritscher & Broadbridge can only be used to model a restricted class of anisotropy. Furthermore, the constitutive equations mean that only a material with anisotropy such that the surface diffusion and diffusivity functions must both be either increasing or decreasing together.
We note that equation (5) can be rewritten as
![]() . (12)
. (12)
A similarity reduction of equation (12) is possible using the scaling group
![]() (13)
(13)
giving invariants
![]() (14)
(14)
This allows the evolution equation (12) to be written as the ordinary differential equation
![]() (15)
(15)
Katoanga and Lisle (personal communications) attempted a partial classification of symmetries for equations (5) and (15) . A total of six classifying equations were found on a 5 parameter group, third order in f and third order in g. The functions for which further symmetries were expected were
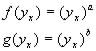 (16a)
(16a)
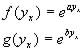 (17a)
(17a)
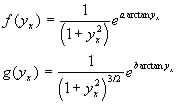 (18a)
(18a)
where a, b are arbitrary constants. Alternatively, these can be written in polar form, remembering that ![]() .
.
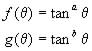 (16b)
(16b)
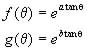 (17b)
(17b)
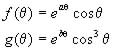 (18b)
(18b)
These functions give the constitutive relations
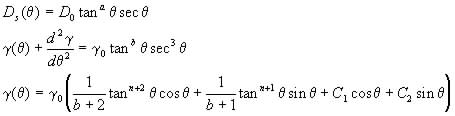 (19)
(19)
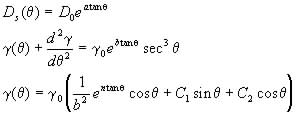 (20)
(20)
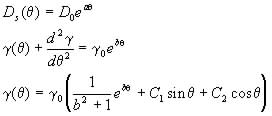 (21)
(21)
The figures at the end of this document provide a useful graphical comparison between the different materials modelled by the constitutive relations. It should be noted that the polar plots of the diffusion and surface tension of the isotropic material gives a circle.