The expressions (15a), (16a), and (17a) were substituted into the evolution equation (15). Using the DIMSYM (Sherring, 1993) routines under Reduce a search was made for point symmetries. Only one generator was found for each case and these are listed below in the same order as (15), (16), and (17) respectively.
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
The existence of only one generator for each set of expressions indicated that the evolution equation (15) could be reduced to at most a third order ODE by use of point symmetries.
It was decided to select one pair expressions (17) for further investigation as the invariants were the simplest to calculate from the generators. More importantly, the constitutive relations (20) display degeneracy and a and b can be chosen such that the surface diffusion and surface tension functions are oppositely increasing and decreasing.
Equation (15) may be simplified to give
![]() (25)
(25)
where ![]() and
and ![]() .
.
From the generator (23) the invariants may be found be solving (Olver, 1993)
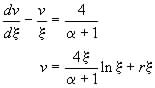
![]() (26)
(26)
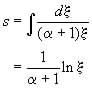 (27)
(27)
Substituting this into equation (25) we get
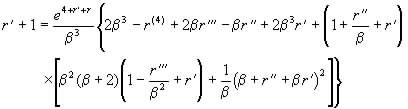 (28)
(28)
where ![]() .
.
Let
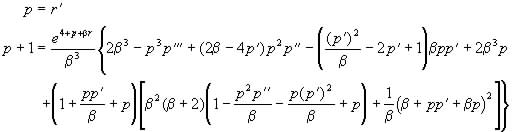 (29)
(29)
The evolution equation (29) is now a third order ODE.